Deriving Quantum Chemical Hamiltonians from Data
- Photophysics of disordered organic systems.
- Deriving quantum chemical hamiltonians from data.
- Design of dyes for imaging of biological systems.
- Design of a light-driven molecular motor.
Overview
Quantum chemistry provides accurate methods for computing the electronic structure of small to medium size molecules, but due to rapid increases in computational cost with system size, applications to large systems is prohibitively expensive. The following two aspects of chemical systems may make computations on large systems computationally feasible:
- Nearsightedness: Interactions between regions of a molecule may be progressively coarse-grained with increasing separation. This enables linear scaling approaches.
- Molecular similarity: Atoms, functional groups, etc. behave similarly in different environments, an assumption which underlies the atom- or group-specific parameters of molecular mechanics and semi-empirical quantum chemistry.
Our goal is to use machine learning algorithms to take better advantage of molecular similarity. Such algorithms can determine useful descriptors of the electronic structures (feature extraction algorithms) and help write the energy and forces as functions of these descriptors (predictors).
The general approach is to first generate a large set of ab initio data on the system of interest, such as a functional group attached to many different molecules or a reaction center in many different environments. This data is then mined for a low-cost model that can reproduce the data with chemical accuracy, but at substantially reduced cost.
In past work, we have applied this approach to develop functional-group specific approaches to electron correlation. The results are analogous to functional-group specific density functionals. This work is summarized in the following video presentation:
Recent work
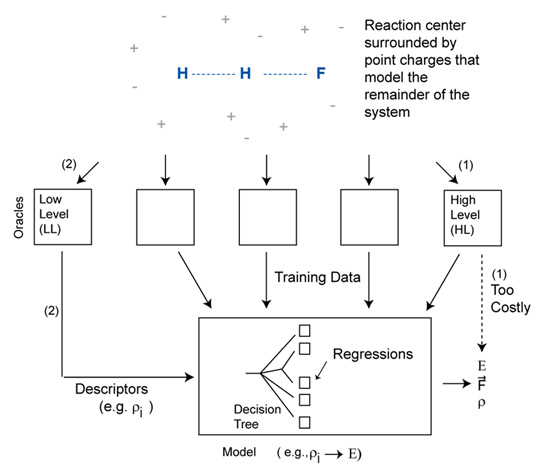
Figure: Schematic representation of a model that is trained to produce the output of a high level model using information generated from low level models.
More recently, we have developed reliable low-cost quantum mechanical models for use in quantum mechanical/molecular mechanical (QM/MM) simulations of chemical reactions. The H + HF → H2 + F collinear reaction was used as a test case. The approach first generates detailed quantum chemical data for the reaction center in geometries and electrostatic environments that span those expected to arise during the molecular dynamics simulations. For each geometry and environment, both high level (HL) and low level (LL) ab initio calculations are performed. A model is then developed to predict the HL results using only inputs generated from the LL theory. The inputs used here are based on principal component analysis of the LL distributed multipoles (DMs), and the model is a simple linear regression. The DMs are monopoles, dipoles and quadrupoles at each atomic center, and summarize the electronic distribution in a manner that is comparable across basis set. The error in the model is dominated by extrapolation from small to large basis sets, with extrapolation from uncorrelated to correlated methods contributing much less error. A single regression can be used to make predictions for a range of reaction-center geometries and environments. For the trial collinear reaction, separate regressions were developed for the entrance channel, transition region, and exit channel. These models can predict the results of QCISD/6-31++G** computations from HF/3-21G DMs, with an average error for the reaction energy profile of 0.47 kcal/mol.