Photophysics of disordered organic systems
- Machine Learning for Chemistry
- Photophysics of disordered organic systems
- Design of dyes for imaging of biological systems
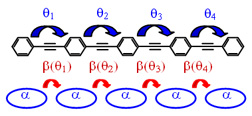
Schematic representation of exciton model used to study effects of disorder.
Overview
Most organic semiconductors share a structural motif in which carbon-carbon single bonds alternate with multiple bonds or aromatic rings. This motif leads to extensive Π-electron delocalization and desirable semiconducting or photophysical properties. This structural motif also imparts flexibility to the system, due to relatively facile rotation about the single C-C bonds. We have been exploring a number of aspects of these low-frequency torsions, including especially effects of disorder in the torsional degrees of freedom on the photophysics.
Spectral lineshapes: Role of torsional entropy
Disorder in the torsional angles of a conjugated polymer plays an important role in establishing the spectral lineshape. The excitation created on absorption of a photon delocalizes over the polymer, due to couplings between aromatic rings, β(θ), that vary with the angle between adjacent rings. The result is a delocalized excitation whose energy, and thus spectral position, is influenced by the torsional angles between the rings over which it is delocalized.
We have shown that an excitation delocalized over N torsional angles has an energy that is primarily a function of the average cosine of these angles:
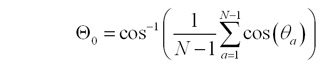
This reduction to a single dimension introduces a configurational entropy (shown below) that can be understood as follows. For an oligomer with two rings, there is a single angle, θ, and all values of Θo are equally probable. For the two angles of an oligomer with three rings, Θo=45° is much more probable than 0° or 90°. (This is analogous to the roll of two die producing an intermediate value of 7 more often than the extreme values of 2 or 12). For large N, the law of large numbers leads to a Gaussian peaked at 45°. The contribution of torsional motion to the line shape in solution can then be obtained from a thermal distribution on a free energy surface that combines the torsional barrier with the configurational entropy. This provides a simple and intuitive model of the lineshapes of conjugated polymer systems. In addition to this torsional entropy effect, disorder also localizes the excitation. We are currently working on a simple but accurate description that includes the effects of both localization and torsional entropy.
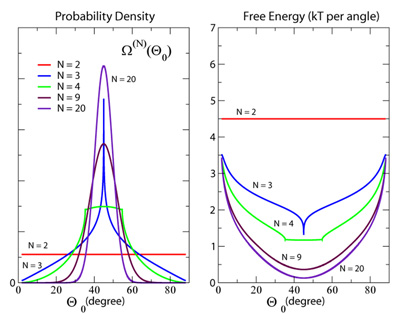
Figure 1: Probability of finding an average angle Θo for an oligomer with N rings (left) and the contribution of the resulting torsional entropy to the free energy (right).
Environmental disorder
Environmental, or outer-sphere disorder, arises from the amorphous nature of the material surrounding the conjugated polymer. In collaboration with Linda Peteanu's group, we have been studying the effects of disorder through a combined experimental/theoretical approach. The electroabsorption spectra measured in the Peteanu group yields the difference in dipole moment, Δμ, and polarizability, Δα, between the ground and first-excited electronic state. For a nominally centro-symmetry polymer, Δμ should be zero. The measured Δμ arises from symmetry breaking and therefore provides a direct handle on the degree of disorder in the sample. Our results show that outer-sphere disorder is at least as important as disorder in the chromophore structure (inner-sphere disorder) in establishing this symmetry breaking.
Effects of aggregation
A new project, in collaboration with the Peteanu group, is a combined experimental/theoretical study of the effects of aggregation on the photophysics of conjugated polymers.