Solutions for a 3-dimensional isotropic harmonic
oscillator in the presence of a stationary magnetic field and an oscillating
electric radiation field.
List of Contents
Unperturbed oscillator
The equation of motion of a particle in a central isotropic harmonic
potential is given by
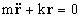
(1)
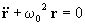
(2a)
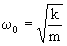 (2b)
(2b)
List of Contents
Effect of a magnetic field: the Zeeman effect
In the presence of a magnetic field (H) the motions of a charged particle
(with charge e) perpendicular to the field are subject to Lorentz forces.
Introducing this force into Eq 1 yields
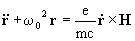
(3)
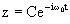
(5)
r
+ = x+iy
(6)
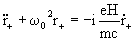 (7)
(7)
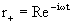
(8)
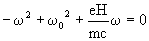
(9)
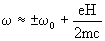
(10)
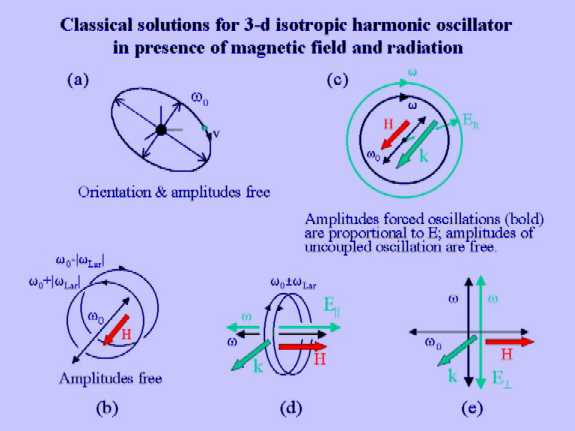
The oscillator emits radiation in all directions. The light emitted
by oscillator with angular frequency w0+|wLar|
and propagating in the direction of the field (towards the reader of Figure
(b, c)) is left circularly polarized. The light emitted by the
same oscillator in the direction opposite to the field (away from the reader)
is right circularly polarized. Accordingly, the polarizations for
w0-|wLar|
are obtained by interchanging left and right in the previous sentence.
Thus, in writing wR and wL
we refer to the sense of rotation observed by looking at the system into
direction –H (This definition of left and right is not based
on the wave vector k, see Figure (b))
List of Contents
Non-resonant interaction with radiation incident
parallel to the applied magnetic field: the Faraday effect also called
Magnetic Circular Birefringence
In the presence of an electric field the equation of motion of the electron
reads
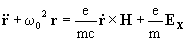
(13)
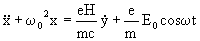
(14a)
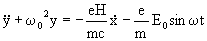 (14b)
(14b)
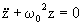 (14c)
(14c)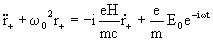 (15)
(15)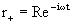
(16)
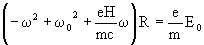 (17)
(17)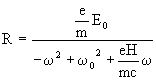 (18)
(18)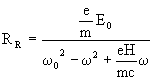 (19)
(19)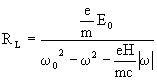 (20)
(20)Let us now consider a material containing a macroscopic number of oscillators
(N per unit of volume). The electronic displacements induced by circularly
polarized light give rise to the electric polarization field
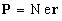
(21)
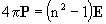
(22a)
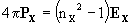
(22b)
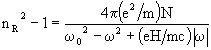
(23a)
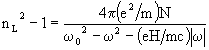
(23b)
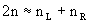
(24)
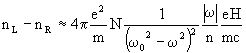
(25)
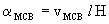
(26)
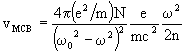
(27)
In summary, MCB results from a difference in the electric polarization
of the medium by L and R circularly polarized light, which originates from
the Zeeman splitting of the electronic energies. The following inequalities
hold: wR < wL,
PR > PL, nR > nL, cR
< cL, irrespective of whether w
is smaller or greater than w0.
L and R are here defined as follows: left is an anti clockwise
rotation of plane polarized light and right a clockwise rotation
when H points to the observer.
List of Contents
Non-resonant interaction with radiation incident
normal to the applied magnetic field: Magnetic Linear Birefringence
Let us consider a beam of monochromatic (frequency w)
linearly
polarized light incident on electronic oscillators of the type described
above, assuming non-resonant conditions, w¹w0.
As in the case of the MCB, the electrons in stationary orbits that are
coupled to the radiation field perform forced motions. Since the electronic
system is cylindrically symmetric along an axis parallel to the magnetic
field (H), all polarization planes of light propagating parallel to H are
equivalent, precluding any birefringence to occur for symmetry reasons.
The situation changes if the light is incident on the oscillator in a direction
perpendicular
to H (Figure (d, e)). The equation of electronic
motion has the same form as in Eq 13,
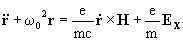
(28)
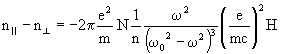
(29)
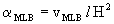
(30)
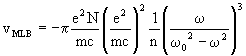
(31)
List of Contents
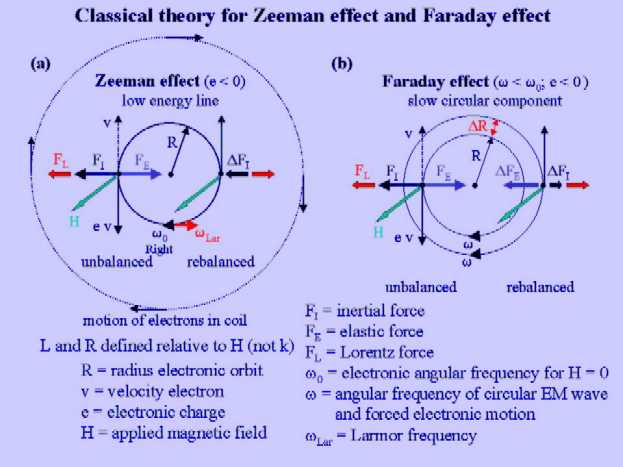
Zeeman effect and Faraday effect: A vector analysis
The effects due to Zeeman (Figure (a)) and Faraday
(Figure (b)) can be interpreted in terms of simple
vector diagrams which depict the electronic orbits and the three forces
involved: the inertial force (FI), the elastic force (FE)
and the Lorentz force (FL). As we consider only stationary circular
solutions for the electronic motion,
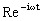
(32)
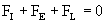
(34)
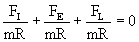
(35)
Substitution of Eqs 33 yields
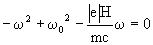
(36)
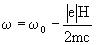
(37)
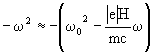
(38)
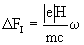
(39)
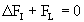
(40)
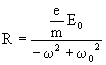
(41)
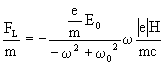
(42)
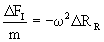
(43)
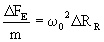
(44)
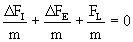
(45)
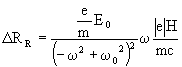
(46)
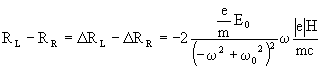
(47)
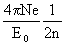
(48)
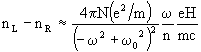
(49)
List of Contents
![]() (2b)
(2b)![]() (4b)
(4b)
![]() (4c)
(4c)![]() (7)
(7)![]() (11b)
(11b)
![]() (12)
(12)![]() (14b)
(14b)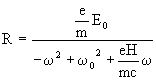 (18)
(18)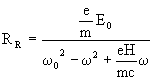 (19)
(19)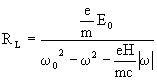 (20)
(20)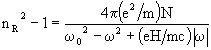 (23a)
(23a)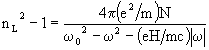 (23b)
(23b)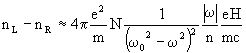 (25)
(25)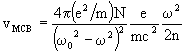 (27)
(27)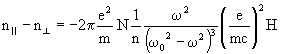 (29)
(29)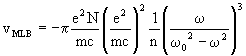 (31)
(31)![]() (33b)
(33b)
![]() (33c)
(33c)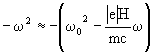 (38)
(38)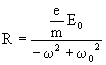 (41)
(41)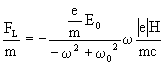 (42)
(42)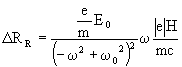 (46)
(46)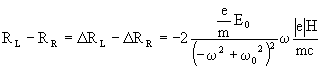 (47)
(47)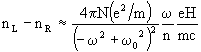 (49)
(49)