| Forcefield Based Simulations |
This chapter concentrates on the static information that can be extracted from the potential energy surface, as well as on the algorithms used for this purpose. The main areas that are covered--minimization and harmonic vibration calculations--are usually lumped together as molecular mechanics, to differentiate them from molecular dynamics calculations (Molecular Dynamics), in which the time evolution of the system is considered.
Related information
Forcefields and Preparing the Energy Expression and the Model focus on the representation of the potential energy surface and the useful ways that it can be biased through the addition of restraints and constraints, as well as other information on preparing the model for calculations.
For specific information on setting up and running minimizations with the various MSI simulation engines, please see the relevant documentation (see Available documentation).
An important method for exploring the potential energy surface is to find configurations that are stable points on the surface. This means finding a point in the configuration space where the net force on each atom vanishes. By adjusting the atomic coordinates and unit cell parameters (for periodic models, if requested) so as to reduce the model potential energy, stable conformations can be identified.
Energy evaluatiom
General minimization process
Minimization of a model is done in two steps. First, the energy expression (an equation describing the energy of the system as a function of its coordinates) must be defined and evaluated for a given conformation. Energy expressions may be defined that include external restraining terms to bias the minimization, in addition to the energy terms.
Next, the conformation is adjusted to lower the value of the energy expression. A minimum may be found after one adjustment or may require many thousands of iterations, depending on the nature of the algorithm, the form of the energy expression, and the size of the model.
Specific minimization example
To introduce the various minimization algorithms, the application of each algorithm to the minimization of a pure quadratic function in two dimensions is discussed. Although the energy surface is most certainly anharmonic in regions away from the minimum, it may be considered to be locally harmonic at the minimum.
Rather than a complex energy expression, the target function used in this illustration is an elliptical surface in two dimensions, as described by Eq. 60:
Eq. 60
Begin with the function and an initial guess of its minimum
This simple function illustrates the properties of the minimization algorithms and captures the mathematical essence of the formulations. Every minimization begins with some energy expression analogous to Eq. 60. In addition to an energy expression defining the energy surface, a starting set of coordinates--an initial guess--for (x,y) must be provided.
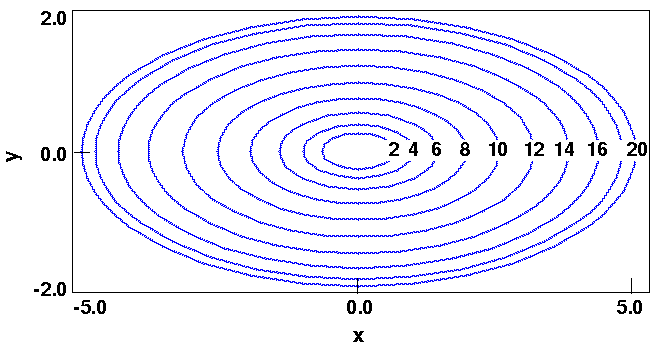
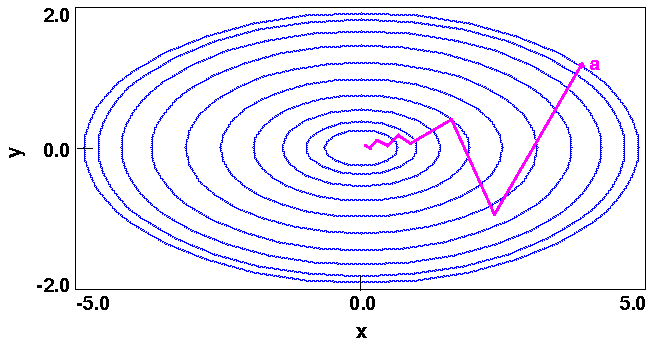
Figure 19 is a contour plot of the energy E in the (x,y) plane. Each ellipse is spaced two energy units apart and represents a locus of points having the same energy. (This is analogous to a contoured topographical map.)
|
Of course, the minimum of this simple function is trivial and can be deduced by inspection to be (0,0).
Given an energy expression that defines the energy surface (such as in Figure 19) and an initial starting point, a minimizer must determine both the direction towards a minimum and the distance to the minimum in that direction. A good initial direction is simply the slope or derivatives of the function at the current point. The derivatives of Eq. 60 are a two-dimensional vector:
Eq. 61
Here, the derivatives are proportional to the coordinates, so that, the further you are from the minimum, the larger the derivatives.
The derivatives, however, merely point downhill and not necessarily towards the minimum (see Figure 20). Thus, as you move in the direction of the initial derivatives, the new derivatives change and point in yet a new direction. In order to improve the efficiency, the more sophisticated algorithms such as conjugate gradients and Newton-Raphson use information on how the derivatives change, to determine the direction.
Line search
Before detailing the different algorithms, the concept of a line search is introduced. Line searches are an implicit component of most minimizers.
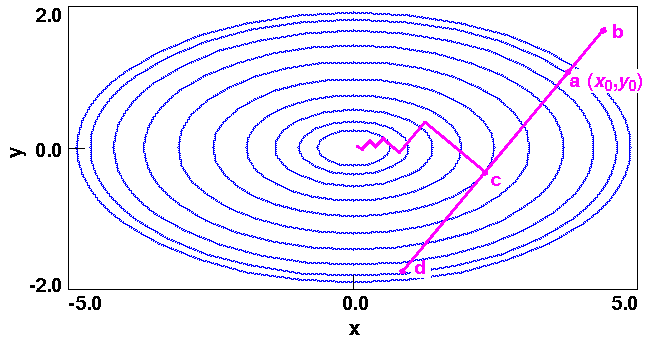
Minimizers usually have two major components. The more generic part is the so-called line search, which actually changes the coordinates to a new lower-energy structure. As an illustration, consider Figure 20
|
In simple terms, a line search amounts to a one-dimensional minimization along a direction vector determined at each iteration. For the path shown in Figure 20, it would be along derivative vector (2x,10y), and the one-dimensional surface can be expressed parametrically in terms of coordinate 
(see also Figure 21):
Eq. 62
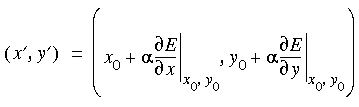where (x´, y´) are coordinates along the line away from the current point (x0, y0) in the direction of the derivative at (x0, y0)., the curve in Figure 21
|
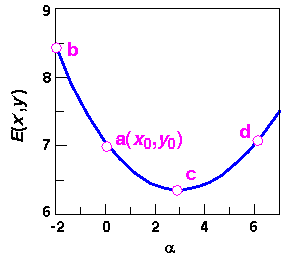
The minimum along (that is, c) coincides with the point at which the line is tangential to the energy contour. Because the maximum derivative's direction is perpendicular to the search line at this point, each line search is orthogonal to the previous one. This is an important property of line searches, which is also included in the discussion of the conjugate gradient algorithm under Conjugate gradient.
Efficiency and cost of extensive line searches
Line searches do not depend on the algorithm that generated the direction vector. The general strategy is to simply bracket the one-dimensional minimum between two points higher in energy, for example points b and d in Figure 21. Then, by a set of successive iterations, the actual minimum is approached (e.g., starting at point a, the first step might lead to b, then the direction might reverse to lead to d and finally to c). Extensive line searches are attractive because they extract all the energy from one direction before moving on to the next. Also, the fact that the new derivatives are always perpendicular to the previous directions produces an efficient path to the minimum for surfaces that are approximately quadratic. In practice, however, line searches are costly in terms of the number of function evaluations that must be performed. The energy must be evaluated at 3-10 points to precisely locate the one-dimensional minimum, and thus extensive line searches are inefficient.
Only minimization algorithms used in MSI's simulation engines (Table 14) are considered here:
Minimization algorithms
| algorithm | variant | simulation engine | |||
|---|---|---|---|---|---|
| CHARMm | Discover | OFF | MMFF93 | ||
|
steepest descents
|
|
|
|
|
|
|
conjugate gradient
|
Polak-Ribiere
|
|
|
|
|
|
|
Fletcher-Reeves
|
|
|
|
|
|
|
Powell
|
|
|
|
|
|
Newton-Raphson
|
full, iterative
|
|
|
|
|
|
|
BFGS (quasi)
|
|
|
|
|
|
|
DFP (quasi)
|
|
|
|
|
|
|
truncated
|
|
|
|
|
|
|
ABNR
|
|
|
|
|
To be consistent in discussions of efficiency, a minimization iteration must be explicitly defined. That is, an iteration is complete when the direction vector is updated. For minimizers using a line search, each completed line search is therefore an iteration. Iterations should not be confused with function evaluations.
Access to controls used to specify what minimizer(s) to use is presented under General methodology for minimization.
Steepest descents
In the steepest-descents method, the line search direction is defined along the direction of the local downhill gradient -
E(xi, yi). Figure 22
Increased efficiency with truncated line searches
What would happen if the line search were eliminated and the position would simply be updated any time that the trial point along the gradient had a lower energy? The advantage would be that the number of function evaluations performed per iteration would be dramatically decreased. Furthermore, by constantly changing the direction to match the current gradient, oscillations along the minimization path might be damped.
|
The exclusive reliance of steepest descents on gradients is both its weakness and its strength. Convergence is slow near the minimum because the gradient approaches zero, but the method is extremely robust, even for systems that are far from harmonic. It is the method most likely to generate a lower-energy structure regardless of what the function is or where the process begins. Therefore, the steepest-descents method is often used when the gradients are large and the configurations are far from the minimum. This is commonly the case for initial relaxation of poorly refined crystallographic data or for graphically built models. In fact, as explained in the following sections, more advanced algorithms are often designed to begin with steepest descents as the first step.
Tip
Conjugate gradient
The reason that the steepest-descents method converges slowly near the minimum is that each segment of the path tends to reverse progress made in an earlier iteration. For example, in Figure 22, each line search deviates somewhat from the ideal direction to the minimum. Successive line searches correct for this deviation, but they cannot efficiently correct because each direction must be orthogonal to the previous direction. Thus, the path oscillates and continually overcorrects for poor choices of directions in earlier steps.
Increasing the efficiency of line searches by controlling the choice of new direction
It would be preferable to prevent the next direction vector from undoing earlier progress. This means using an algorithm that produces a complete basis set of mutually conjugate directions such that each successive step continually refines the direction toward the minimum. If these conjugate directions truly span the space of the energy surface, then minimization along each direction in turn must by definition end in arriving at a minimum. The conjugate gradient algorithm constructs and follows such a set of directions.
i:
Eq. 63
Polak-Ribiere method
where
i is a scalar that can be defined in two ways. In the Polak-Ribiere method, i is defined as:
Eq. 64
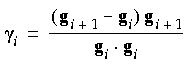Fletcher-Reeves method
And in the Fletcher-Reeves method (1964),
i is defined as:
Eq. 65
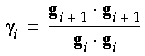(Fletcher 1980). Although the two conjugate gradient methods have similar characteristics, one or the other might behave better in certain cases.
The Powell method (used in CHARMm and Cerius2·MMFF; see Powell 1977 and Gunsteren & Karplus 1980) is essentially a strategy for handling convergence problems.
Conjugate gradients is the method of choice for large models because, in contrast to Newton-Raphson methods, where storage of a second-derivative matrix (N (N + 1) \xda 2) is required, only the previous 3N gradients and directions have to be stored. However, to ensure that the directions are mutually conjugate, more complete line search minimizations must be performed along each direction. Since these line searches consume several function evaluations per search, the time per iteration may be longer for conjugate gradients than for steepest descents. This is more than compensated for by the more efficient convergence to the minimum achieved by conjugate gradients.
Tip
|
The conjugate gradient method can be unstable if the conformation is so far away from a local minimum that the potential energy surface is not nearly quadratic. Steepest descents (Steepest descents) should generally be used for the first 10-100 steps of minimization. Please see also When to use different algorithms. |
Newton-Raphson methods
Iterative Newton-Raphson method
Using the second derivatives to accelerate convergence
As a rule, N 2 independent data points are required to numerically solve a harmonic function with N variables. Since a gradient is a vector N long, the best you can hope for in a gradient-based minimizer is to converge in N steps. However, if you can exploit second-derivative information, a minimization could ideally converge in one step, because each second derivative is an N X N matrix. This is the principle behind the variable metric minimization algorithms, of which Newton-Raphson is perhaps the most commonly used.
Eq. 66
where rmin is the predicted minimum, r0 is an arbitrary starting point, A(r0) is the matrix of second partial derivatives of the energy with respect to the coordinates at r0 (also known as the Hessian matrix), and E(r0) is the gradient of the potential energy at r0.
The energy surface is generally not harmonic, so that the minimum-energy structure cannot be determined with one Newton-Raphson step. Instead, the algorithm must be applied iteratively:
Eq. 67
Thus, the ith point is determined by taking a Newton-Raphson step from the previous point (i - 1). Similar to conjugate gradients, the efficiency of Newton-Raphson minimization increases as convergence is approached (Ermer 1976).
As elegant as this algorithm appears, its application to molecular modeling has several drawbacks. First, the terms in the Hessian matrix are difficult to derive and are computationally costly for molecular forcefields. Furthermore, when a structure is far from the minimum (where the energy surface is anharmonic), the minimization can become unstable.
Tip
|
The iterative Newton-Raphson method can be unstable if the conformation is so far away from a local minimum that the potential energy surface is not nearly quadratic. Steepest descents (Steepest descents) should generally be used for the first 10-100 steps of minimization. Please see also When to use different algorithms. |
Variants of iterative Newton-Raphson method
In addition to the iterative Newton-Raphson method, variants of the Newton method are available (Table 14): the quasi-Newton (which includes the BFGS and DFP methods) and the truncated Newton methods. These variants, as well as others, are characterized by the use of the general algorithm shown in Figure 24.
|
The differences among the various Newton methods revolve around:
k).
Of the several different updating schemes for determining B, the two most common ones are the Broyden, Fletcher, Goldfarb, and Shanno (BFGS, also known as VA09A) and the Davidon, Fletcher, and Powell (DFP) algorithms. The BFGS method uses a Fletcher-Powell algorithm with approximate second derivatives.
DFP updating scheme
Defining
and as the changes in the coordinates and gradients for successive iterations, the approximate Hessians (B-1) are given by the following in the DFP method:
Eq. 68
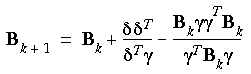BFGS updating scheme
and in the BFGS method:
Eq. 69
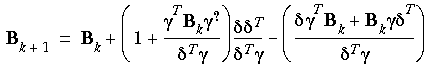In practice, the BFGS method is preferred over the DFP method, because BFGS has been shown to converge globally with inexact line searches, while DFP has not.
The quasi-Newton-Raphson method has an advantage over the conjugate-gradient method in that it has been shown to be quadratically convergent for inexact line searches. Like the conjugate-gradient method, the method also avoids calculating the Hessian. However, it still requires storage proportional to N 2 (N = number of degrees of freedom), and the updated Hessian approximation may become singular or indefinite even when the updating scheme guarantees hereditary positive-definiteness. Finally, the behavior may become inefficient in regions where the second derivatives change rapidly. Thus, this minimizer is used in practice as a bridge between the iterative Newton-Raphson and the conjugate-gradient methods.
Tip
|
The quasi Newton-Raphson method can be unstable if the conformation is so far away from a local minimum that the potential energy surface is not nearly quadratic. Steepest descents (Steepest descents) should generally be used for the first 10-100 steps of minimization. Please see also When to use different algorithms. |
Truncated Newton-Raphson
The truncated Newton-Raphson method (Figure 25) differs from the quasi-Newton-Raphson method in two respects:
By using the second derivatives to generate the Hessian, the minimization is more stable far away from the minimum or in regions where the derivatives change rapidly. Since solving Eq. 67 by inversion is not tractable for large models, the search direction is solved iteratively using the conjugate-gradient method. Furthermore, to increase the speed in solving the search direction, the tolerance for conjugate-gradient convergence is dependent on the proximity to the minimum. The tolerance is relatively large when the minimization is far from the solution and decreases during convergence. This is appropriate, because the dependency of convergence on the line search direction becomes greater at the end of the minimization. At the beginning, it is more efficient to take more less-well-defined Newton steps than to take fewer well-defined steps.
To further increase the convergence rate of the conjugate-gradient minimization, the Newton equation that is solved for each line search direction is preconditioned with a matrix M. The matrix M may range in complexity from the identity matrix (M = I) to M = H. In the first limit, the Newton equation remains unchanged. However, in the second, there is no saving in computational effort, because M-1 H = I must be solved.
ABNR similar to truncated Newton-Raphson
The adopted-basis Newton-Raphson method (ABNR) is similar to the truncated Newton-Raphson method. The ABNR method performs energy minimization using a Newton-Raphson algorithm applied to a subspace of the coordinate vector spanned by the displacement coordinates of the last positions. The second derivative matrix is constructed numerically from the change in the gradient vectors, and is inverted by an eigenvector analysis that allows the routine to recognize and avoid saddle points in the energy surface. At each step, the residual gradient vector is calculated and used to add a steepest-descents step, incorporating new direction into the basis set.
Many issues are involved in designing an appropriate simulation strategy for a given model, some of which have to do only with the minimization algorithms themselves:
General methodology for minimization
Prerequisites
One of the most important steps in any simulation is properly preparing the model to be simulated. Calculations on the fastest computer running the most efficient minimization algorithm may be worthless if the hydrogen is put on the wrong nitrogen or an important water molecule is omitted.
To set up a minimization run, first:
2. Set up the forcefield and prepare your model (Preparing the Energy Expression and the Model).
Accessing minimization controls
Next:
4. Specify the desired output:
Finally:
For specific information on setting up and running minimizations with the various MSI simulation engines and on examining the results, please see the relevant documentation (see Available documentation).
When to use different algorithms
The default minimizers in Discover and OFF use a cascade of appropriate minimization algorithms in sequence. However, you may want to exercise more control over your simulation.
The choice of which algorithm to use depends on two factors--the size of the model and its current state of optimization. The conjugate gradient and steepest descents methods can be used with models of any size. Most Newton-Raphson methods cannot be used with very large models, because they need sufficient disk space to store a second-derivative matrix. (The ABNR method does not store a large second-derivative matrix.)
For highly distorted structures, the presence of cross terms and Morse bond potentials in the forcefield can cause convergence problems. These functional forms can produce either small restoring forces or, more seriously, minima at nonphysical points on the potential energy surface.
Conjugate gradient vs. Newton-Raphson and disk space
Several practical aspects of the conjugate gradient method are worth mentioning. First, the conjugate gradient algorithm requires convergence along each line search before continuing in the next direction. The gradient at step i+1 must be perpendicular to hi or the derivation guaranteeing a conjugate set of directions breaks down. Second, to start conjugate gradients, an initial direction h0 must be chosen that is equal to the initial gradient. Finally, additional storage is required for an extra vector of N elements to hold the N components of the old gradient. For energy minimization in Cartesian space this would be the 3N derivatives of the energy with respect to the x, y, and z coordinates of each atom. This makes conjugate gradient the method of choice for systems that are too large for storing and manipulating a second-derivative matrix, as is required by the Newton-Raphson minimizers.
| 1
N = number of atoms (number of degrees of freedom).
|
Also, note that the derivation invokes a quadratic approximation. For nonharmonic systems, the conjugate gradient method can exhaustively minimize along the conjugate directions without converging. This condition indicates that the minimizer may have gotten stuck at a saddle point. If this occurs, you can restart the algorithm. Several minimizations may be required. For a detailed discussion of this algorithm, see the excellent text by Press et al. (1986) or the somewhat more formal treatment by Fletcher (1980).
Convergence criteria
Mathematical definition
In the literature a wide variety of criteria have been used to judge minimization convergence in molecular modeling. Mathematically, a minimum is defined as the point at which the derivatives of the function are zero and the second-derivative matrix is positive definite. Nongradient minimizers can use only the increment in the energy and/or coordinates as criteria. In gradient minimizers, derivatives are available analytically and should be used directly to assess convergence.
In a molecular minimization, the atomic derivatives may be summarized as an average, a root-mean-square (rms) value, or the largest value. The average, of course, must be an average of the absolute values of the derivatives, because the distribution of derivatives is symmetric about zero. A rms derivative is a better measure than the average, because it weights larger derivatives more, and it is therefore less likely that a few large derivatives would escape detection, which can occur with simple averages.
The more difficult question is, What value of the average or rms derivative constitutes convergence? The specific value depends on the objective of the minimization. If you simply want to relax overlapping atoms before beginning a dynamics run, minimizing to a maximum derivative of 1.0 kcal mol-1 Å-1 is usually sufficient. However, to perform a normal mode analysis, the maximum derivative must be less than 10-5, or the frequencies may be shifted by several wavenumbers.
There is no guarantee that the minimum you find is necessarily a global minimum.
You generally also set a maximum number of iterations, so that runs that do not converge will nevertheless end within a reasonabe amount of time. That is, the run ends when either the convergence criteria or the maximum number of iterations is reached, whichever occurs first.
Significance of minimum-energy structure
Calculated energy is relative
In dealing with macromolecular optimization calculations, it is important to keep in mind the theoretical significance of the minimum-energy structure and its calculated energy. For all forcefields used in calculations of this type, the energy zero is arbitrary, and therefore, the total potential energy of different models cannot be compared directly. However, it is meaningful to make comparisons of energies calculated for different configurations of chemically identical models. In principle, the calculated energy of a fully minimized structure is the classical enthalpy at absolute zero, ignoring quantum effects (in particular the zero-point vibrational motion). For a model that is sufficiently small that its normal modes can be calculated, quantum corrections for zero-point energy and the free energy at higher temperatures can be taken into account (Hagler et al. 1979c).
The relative importance of these fundamental considerations depends on the objective of the calculation. When studying the relative binding in an enzyme active site of two substrates, one of which is flexible and the other rigid, entropic effects may be crucial for obtaining even qualitative agreement with experimental binding constants. On the other hand, if a putative compound overlaps sterically with many active-site atoms and causes hundreds of kilocalories of strain energy even in a minimized structure, the compound can be rejected confidently.
An energy calculation is essentially just a zero-iteration minimization. It is used to calculate the energy of the current model structure without changing any atom positions.
Energy and gradient calculation
To specify single-point energy and gradient calculations rather than a minimization (Minimizations with MSI simulation engines):
Harmonic vibrational frequencies obtained from an equilibrium geometry
The vibrational frequencies and modes of a molecule are strictly dynamic properties. However, it is possible to calculate the harmonic vibrational frequencies of a model from just information at its equilibrium geometry by expanding the potential energy surface as a Taylor series, truncating after the second term, and considering infinitesimal displacements. This harmonic approximation usually gives a good description of the true frequencies and normal modes and can be valuable for tasks ranging from evaluating the quality of a forcefield to understanding vibrational shifts induced by conformational changes or other interactions. The harmonic vibrational frequencies also can be used for zero-point vibrational corrections and for deriving vibrational free energy contributions. These effects can be important in comparing conformational energies and rotational barrier heights.
Beyond these considerations, the vibrational frequencies can be used for two classes of problems:
Following Wilson et al. (1980), the kinetic energy of the nuclei is:
Eq. 70
where the coordinates represent displacements from an equilibrium structure. If the 3N Cartesian coordinates are replaced with 3N mass-weighted coordinates as follows:
Eq. 71
Simplified kinetic energy of nuclei
where m
is the mass of the atom associated with the coordinate, and 
x runs over the y and z coordinates, as well as x, then the kinetic energy has the following simple form:
Eq. 72
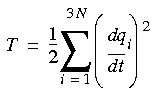The second term in a Taylor series is needed to obtain vibrational information
When the potential energy of the system is expanded as a Taylor series in the same coordinates, it yields:
Eq. 73
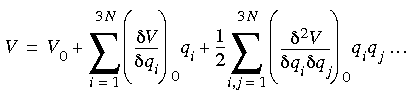V0 is simply a constant--the energy scale can be chosen so that V0 = 0. The definition of an equilibrium structure is that the force on each atom is zero. The second term in Eq. 73 also is zero, leaving the following second-order approximation of the potential energy:
Eq. 74
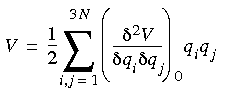Combining energy and motion and solving for the mass-weighted coordinates
Using this approximation of the potential energy in Newton's equations of motion (Eq. 4) yields the following simultaneous second-order differential equations:
Eq. 75
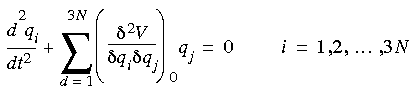The solution to these equations can be of the form:
Eq. 76
Numerically solvable form of the function
where the Ai are related to the relative amplitudes of the vibrational motion, 
1\xda 2 is proportional to the vibrational frequency, and is a phase. Substituting Eq. 76 in Eq. 75 yields a set of algebraic equations:
Eq. 77
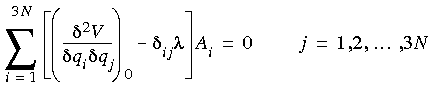where ij is a Kronecker delta, which equals one if i = j and zero otherwise. This is an eigenvalue problem that is readily solved numerically by standard techniques. The second derivatives of the potential energy, often called the force constants, can be analytically evaluated for most energy expressions used in molecular mechanics, in terms of the Cartesian coordinates of the atoms. A simple transformation to the mass-weighted coordinates then gives the values needed in Eq. 77.
Vibrational frequencies
Eigenvalues converted to vibrational frequencies
The simulation engine determines vibrational frequencies by calculating the second derivative matrix, mass weighting it, and then diagonalizing it to obtain the eigenvalues. These eigenvalues are then converted to vibrational frequencies in wavenumbers as follows:
Eq. 78
Evaluating the quality of the calculation
where the conversion factor F converts the units from kcal mol-1 to wavenumbers. Of the 3N coordinates used to calculate the energy and vibrational frequencies, six correspond to net translations and rotations of the model (five for linear systems). These six modes have no restoring force and therefore have vibrational frequencies of zero for a minimized structure. Due to numerical inaccuracies, the simulation engine reports these frequencies with small values, which are typically less than 0.1 cm-1. If the structure is not perfectly minimized, the first-order terms in the Taylor expansion of the potential surface in Eq. 73 do not vanish. In turn, they introduce terms that couple the net rotations of the model with the internal motions and both perturb the internal vibrational frequencies and give apparent frequencies for the three rotations. Thus, the magnitude of the six "zero" frequencies is a good indication of the quality of the calculation.
Transition states
The model must be optimized before doing a vibration calculation
For calculating vibrational frequencies, the model must be minimized and the gradients must be zero. This does not mean that the configuration of the model must be at a minimum, but rather that it must be at a stable point on the surface. If the structure is not at a minimum, but rather is at a saddle point or transition state in one or more directions, this is reflected in the eigenvalues and the reported vibrational frequencies. For a saddle point, at least one eigenvalue is negative, which means that the curvature of the surface along at least one normal mode is negative. By convention, the imaginary frequencies for such modes are reported as negative.
Thermodynamics
Quantum mechanical solution...
The quantum mechanical solution for the vibrational energy of a set of uncoupled harmonic oscillators, which corresponds to the classical treatment outlined above, is:
Eq. 79
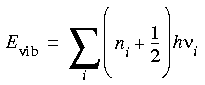...used to correct the vibrational energy determined with a forcefield
where the summation is over all the vibrational frequencies, ni is the vibrational quantum number for each vibration, h is Planck's constant, and
i is the vibrational frequency. This leads to the following correction to the classical forcefield energy:
Eq. 80
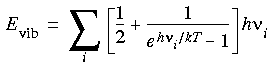Free energy correction
where k is the Boltzmann constant and T is the temperature. The first term, h
i \xda 2, is the zero-point correction; the second term corrects for the average thermal population of vibrational levels at the temperature T. This leads to a vibrational free energy correction of:
Eq. 81
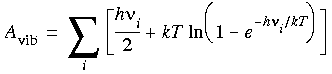Vibrational entropy
and a vibrational entropy of:
Eq. 82
General methodology for vibrational calculations
Specifying a vibration calculation
To specify a vibration calculation for a model that is already well minimized (Minimizations with MSI simulation engines):
Computation of the harmonic vibrational frequencies requires the storage and diagonalization of the second-derivative matrix, which has dimensions of 3N X 3N, where N is the number of atoms. The work involved in the diagonalization scales as N 3 and quickly becomes prohibitively expensive for more than a few hundred atoms. The frequencies are valid only for well minimized models having maximum derivatives no greater than approximately 0.001 kcal mol-1 Å-1.
The forcefield is a major consideration. Most forcefield development has emphasized structures and energetics rather than vibrational frequencies. As a result, the frequencies calculated with forcefields (see Forcefields) such as AMBER, MM2, CHARMm, and, to a lesser extent, CVFF, may often be in error by several hundred wavenumbers. The inclusion of cross terms such as bond-bond and bond-angle terms is crucial for the accurate reproduction of experimental frequencies. The CVFF forcefield includes such cross terms and was, in part, parameterized to reproduce experimental frequencies, which explains its moderately good performance for vibrational calculations. The second-generation forcefields MM3 and CFF were explicitly designed to evenly weight vibrational frequencies as well as structural and energetic properties. Therefore, they provide the most reasonable and consistent results, usually within 50-100 cm-1. This error of up to approximately 100 cm-1 appears to be the current limit of general-purpose, transferable forcefields.
) and exit if true.
